Q* Search: Heuristic Search with Deep Q-Networks

Forest Agostinelli, Shahaf Shperberg, Alexander Shmakov, Stephen McAleer, Roy Fox, and Pierre Baldi

Bridging the Gap Between AI Planning and Reinforcement Learning workshop (PRL @ ICAPS), 2024

BibTeX

@conference{ Agostinelli2024Qstar,
  Title = "{Q}* Search: Heuristic Search with {D}eep {Q}-{N}etworks",
  Author = "Forest Agostinelli and Shahaf Shperberg and Alexander Shmakov and Stephen McAleer and Roy Fox and Pierre Baldi",
  Booktitle = "Bridging the Gap Between AI Planning and Reinforcement Learning workshop (PRL @ ICAPS)",
  Year = "2024"
}

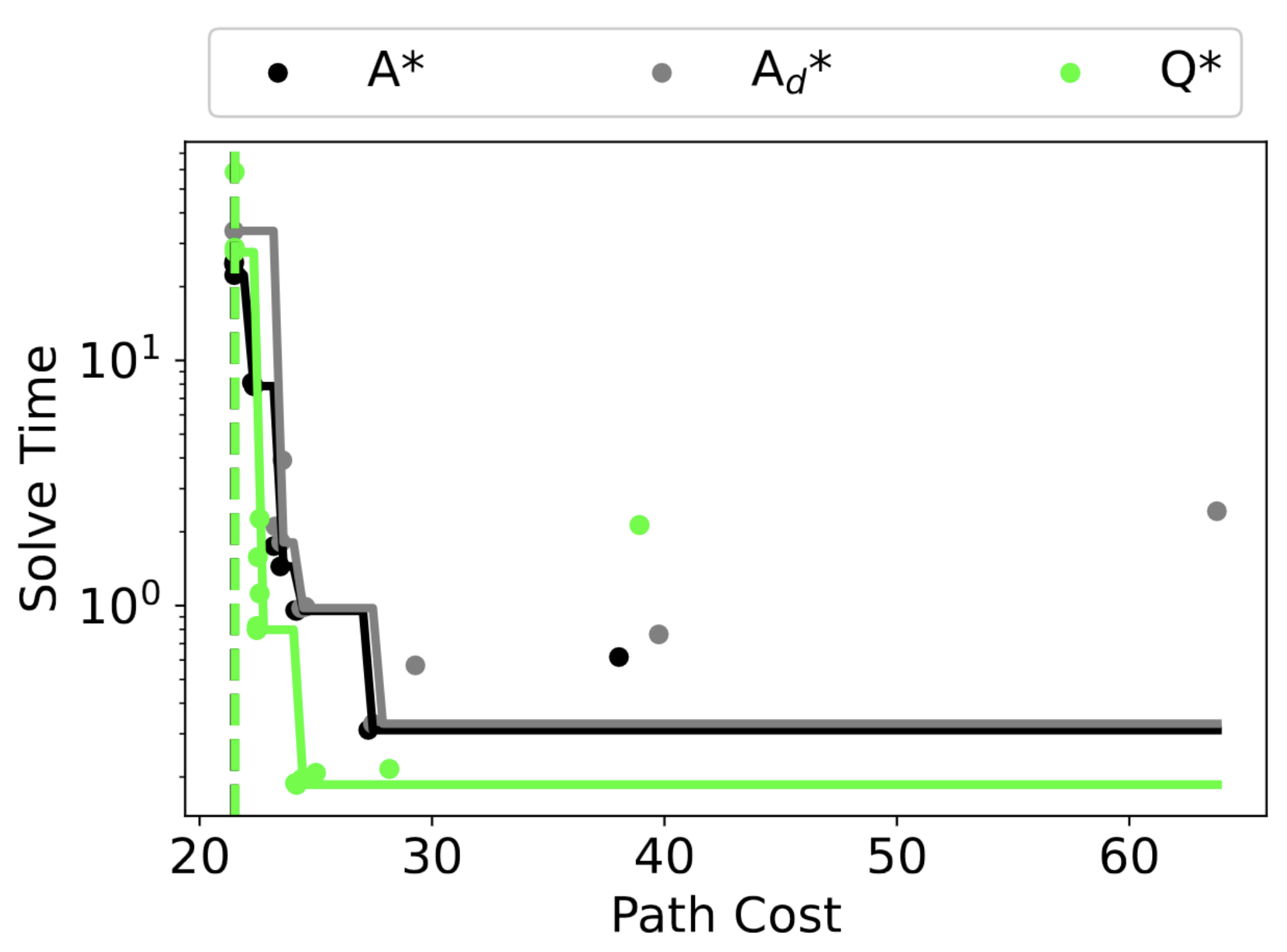
Efficiently solving problems with large action spaces using A* search has been of importance to the artificial intelligence community for decades. This is because the computation and memory requirements of A* search grow linearly with the size of the action space. This burden becomes even more apparent when A* search uses a heuristic function learned by computationally expensive function approximators, such as deep neural networks. To address this problem, we introduce Q* search, a search algorithm that uses deep Q-networks to guide search in order to take advantage of the fact that the sum of the transition costs and heuristic values of the children of a node can be computed with a single forward pass through a deep Q-network without explicitly generating those children. This significantly reduces computation time and requires only one node to be generated per iteration. We use Q* search on different domains and action spaces, showing that Q* suffers from only a small runtime overhead as the action size increases. In addition, our empirical results show Q* search is up to 129 times faster and generates up to 1288 times fewer nodes than A* search. Finally, although obtaining admissible heuristic functions from deep neural networks is an ongoing area of research, we prove that Q* search is guaranteed to find a shortest path given a heuristic function does not overestimate the sum of the transition cost and cost-to-go of the state.