Independent Natural Policy Gradient Always Converges in Markov Potential Games

Roy Fox, Stephen McAleer, William Overman, and Ioannis Panageas

25th International Conference on Artificial Intelligence and Statistics (AISTATS), 2022

BibTeX

@conference{ Fox2022MPG,
  Title = "Independent Natural Policy Gradient Always Converges in {M}arkov {P}otential {G}ames",
  Author = "Roy Fox and Stephen McAleer and William Overman and Ioannis Panageas",
  Booktitle = "25th International Conference on Artificial Intelligence and Statistics (AISTATS)",
  Year = "2022"
}

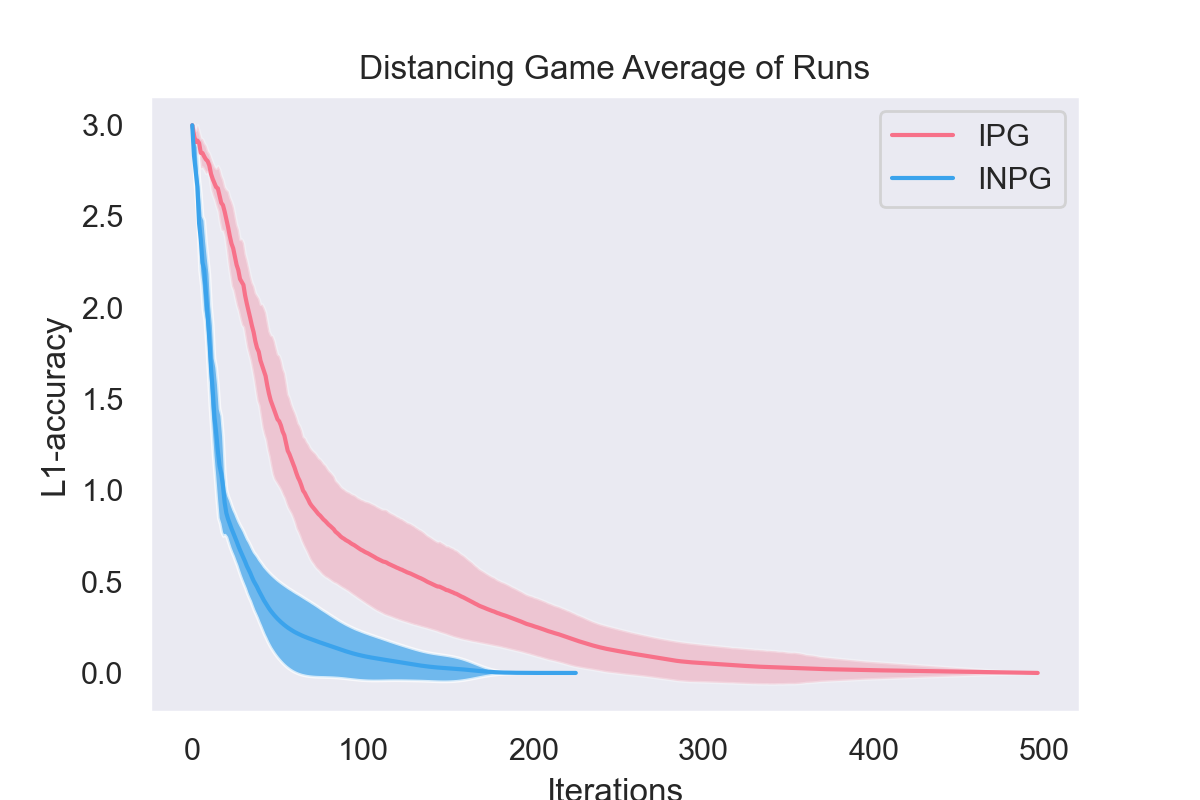
Natural policy gradient has emerged as one of the most successful algorithms for computing optimal policies in challenging Reinforcement Learning (RL) tasks, but very little was known about its convergence properties until recently. The picture becomes more blurry when it comes to multi-agent RL (MARL), where only few works have theoretical guarantees for convergence to Nash policies. In this paper, we focus on a particular class of multi-agent stochastic games called Markov Potential Games and prove that Independent Natural Policy Gradient always converges using constant learning rates. The proof deviates from existing approaches and overcomes the challenge that Markov potential Games do not have unique optimal values (as single-agent settings exhibit), leading different initializations to different limit point values. We complement our theoretical results with experiments that indicate that Natural Policy Gradient outperforms Policy Gradient in multi-state congestion games.